Bestimmungswörter:
-faktor Verhältnisse von gleichartigen linearen Größen (Einheit: 1) - geben den Faktor an, mit dem eine Größe zu multiplizieren ist, um ihre Abweichung von einer Ausgangsgröße zu berücksichtigen (z.B.: Schallreflexionsfaktor r)
-grad Verhältnisse von quadratischen Größen, deren Maximalwert 1 (=100%) nicht überschreitet (z.B.: Schalldissipationsgrad ![]() )
)
-koeffizient Größe, die den Einfluß einer Stoffeigenschaft oder eines physikalischen Systems auf einen physikalischen Zusammenhang kennzeichnet (z.B.: Schalldämpfungskoeffizient α, Abklingkoeffizient δ , Adiabatenkoeffizient χ)
-konstante universelle, unveränderliche Größe, die den Zustand oder das Verhalten von Stoffen oder Systemen beschreibt (z.B.: Dämpfungskonstante b)
-maß logarithmierte Verhältnisse von Größen mit gleicher Einheit (z.B.: Abklingmaß Λ)
-modul Kehrwert von Koeffizienten (z.B.: Elastizitätsmodul E , Kompressionsmodul K)
-pegel logarithmierte Verhältnisse von Größen mit gleicher Einheit mit definierter Bezugsgröße im Nenner (z.B.: Lautstärkepegel LS)
-zahl (z.B.: Brechzahl n , Mach-Zahl M)
|
Größe |
Formelzeichen |
Einheit |
Ableitung |
| Abklingkoeffizient | δ | 1/s | δ = b / 2m = Λ / T |
| Abklingmaß | Λ | 1 [dB] | Λ = 20 lg k dB |
| Abklingzeit | τ | s | τ = 1 / δ |
| Absorptionsexponent | α' | 1 | α' = - ln (1 - |
| Adiabatenkoeffizient | Χ | 1 | |
| äußere Kraft | Fext. | N | |
| akustische Impedanz | Za | Ns/m5 | Za = p / q |
| Amplitude | A | m | A = ymax. |
| resultiernde ~ | Ar | m | |
| Anzahl | n | 1 | n = 1, 2, 3, ... |
| Ausbreitungskoeffizient | γ | 1/m | γ = α + i · β |
| Brechungswinkel | β | rad | |
| Brechzahl | n | 1 | n = sin α / sin β = c1 / c2 |
| Dämpfungsverhältnis | k | 1 | k = A(t) / A(t + T) |
| Dämpfungsgrad | D | s | D = δ / ω = d / 2 |
| Dämpfungskonstante | b | kg/s | |
| Dämpfungsmaß | D | 1 [dB] | D = αL · x |
| Dehnung | ε | 1 | ε = σ / E |
| Dehnungszahl | α | m2/N | α = 1 / E |
| Dichte | kg/m3 | ||
| Durchmesser | d | m | |
| durchschallte Fläche | S | m2 | |
| Einfallswinkel | αe | rad | |
| Einschwingzeit | s | ||
| Elastizitätsmodul | E | N/m2 | E = σ / ε |
| Elongation | y | m | y = A · sin |
| Frequenz | f | Hz | f = 1 / T |
| ~ der Grundschwinung | f0 | Hz | |
| ~ der Schallquelle | fq | Hz | |
| ~ beim Beobachter | fb | Hz | |
| resultierende ~ | fr | Hz | fr = (f1 + f2) / 2 |
| Schwebungs~ | fS | Hz | fS = |f1 - f2| |
| Eigen~ | fe | Hz | |
| Anregungs~ | fa | Hz | |
| Frequenzindex | Fi | oct | F = ld (f / f0) oct (f0=125 Hz) |
| Frequenzmaßintervall | m | oct | m = ld (f1 / f2) = 3,322 lg (f1 / f2) |
| terz | m = 3 ld (f1 / f2) = 9,966 lg (f1 / f2) | ||
| Savart | m = 300 ld (f1 / f2) = 9996,5 lg (f1 / f2) | ||
| Millioktave | m = 1000 ld (f1 / f2) = 3321,9 lg (f1 / f2) | ||
| Cent | m = 1200 ld (f1 / f2) = 3986,3 lg (f1 / f2) | ||
| dec | m = ld (f1 / f2) (jeweils f1 > f2) | ||
| Gangunterschied | δ | m | δ = (Δδ / 2) λ |
| Gesamtschallpegel | LG | 1 [dB] | LG = L1 + LZ |
| Geschwindigkeit des Beobachters | vb | m/s | |
| Güte | Q | 1 | Q = 1/d = 1/2D |
| Hallmaß | R | 1 [dB] | R = 10 lg Jr / Jdirekt |
| Kompressibilität | k | m2/N | k = 1 / K |
| Kompressionsmodul | K | N/m2 | K = E / [3·(1-2v)] |
| Klarheitsmaß | C | 1[dB] | |
| Kraft | F | N | |
| Kreisfrequenz | ω | rad/s | ω = 2πf |
| Länge | l | m | |
| Lautheit | S | sone | S = 20,1(Ls -40) sone |
| Lautstärkepegel | LS | 1 [dB] | LS = 10 lg (J / J0) |
| Phon | Phon = dB bei 1 kHz | ||
| logarithmisches Dekrement | Λ | 1 | Λ = ln K = δT |
| Machzahl | M | 1 | M = c / vq |
| Masse | m | kg | |
| Tonheit | z | mel oder Bark | 1 Bark = 100 mel |
| Nachhallzeit | TH | s | TH = 0,163 [V / ( |
| Normalspannung | σ | N/m2 | σ = E · ε = F / S |
| Ort (Abstand, Entfernung) | x | m | |
| ...pegel | L | 1 [dB] | |
| Periodendauer | T | s | T = 1 / f = |
| Phasenkoeffizient | β | ||
| Phasenwinkel (Phasenverschiebung) | rad | ||
| Poissonzahl | μ | 1 | μ = 1 / ν |
| Querdehnungszahl | ν | 1 | |
| Querschnitt(sfläche) | S | m2 | |
| Reflexionswinkel | αr | rad | |
| Schallabsorptionsgrad | α | 1 | α = (Je - Jr) / Je |
| Schalldämm-Maß | R | 1[dB] | R = 10 lg (Pe / Pr) |
| Schalldämpfungskoeffizient | α | 1/m | |
| Schalldichte | E | J/m3 | E = J / c |
| Schalldichtepegel | LE | 1 [dB] | |
| Schalldissipationsgrad | δ | 1 | δ = Ja / Je |
| Schalldruck | p | Pa | |
| ~amplitude | pmax. | Pa | |
| effektiver ~ | peff. | Pa | 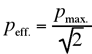 |
| statischer Druck | peff.,0 | Pa | peff.,0 = 2 · 10-5 Pa |
| einfallender ~ | pe | Pa | |
| reflektierter ~ | pr | Pa | |
| ~pegel | Lp | 1 | Lp = 10 lg (peff.2 / peff.,02) = 20 lg (peff. / peff.,0) |
| Schallfluss | q | m3/s | q = v · S |
| Schallgeschwindigkeit | c | m/s | c = |
| Schallintensität | J | W/m2 | J = w · c |
| absorbierte ~ | Ja | W/m2 | |
| durchgelassene ~ | Jd | W/m2 | |
| einfallende ~ | Je | W/m2 | |
| reflektierte ~ | Jr | W/m2 | |
| Bezugs~ | J0 | W/m2 | L0 = 10-12W / m2 |
| ~spegel | LJ | 1 [dB] | |
| Schallkennimpedanz | Z | kg/(m2s) | |
| Schalleistung | P | W | P = J · S |
| durchgelassene ~ | Pd | W | |
| einfallende ~ | Pe | W | |
| ~spegel | LP | 1 [dB] | LP = 10 lg (P / P0) |
| Schallpegeldifferenz | 1 [dB] | ||
| Schallpegelzuschlag | LZ | 1 [dB] | |
| Schallquellengeschwindigkeit | vq | m/s | |
| Schallreflexionsfaktor | r | 1 | r = pr / pe |
| Schallreflexionsgrad | 1 | ||
| Schallschnelle | v | m/s | |
| ~amplitude | vmax. | m/s | |
| effektive ~ | veff. | m/s | 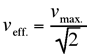 |
| ~pegel | Lv | 1 [dB] | |
| Schalltransmissionsgrad | τ | 1 | τ = Jd / Je |
| spetifische Gaskonstante | Ri | J / (K kg) | |
| Temperatur | ϑ | K oder °C | |
| Verlustfaktor | d | 1 | d = 2D = 2δ / ω |
| Volumen | V | m3 | |
| Wellenlänge | λ | m | λ = c / f = c · T |
| ~ der Grundschwingung | λ0 | m | |
| ~ des n. Partialtons | λn | m | |
| Wellenzahl | k | 1 /m | k = 1 / λ |
| Kreis~ | k | 1 /m | k = 2π / λ = ω · c |
| Zeit | t | s |
=> zum Inhalt
=> zum Inhalt

=> zum Inhalt
|
Einheit |
Benennung |
Größe |
Ableitung |
für |
Formelzeichen |
| m | Meter | Länge | - | Elongation | y |
| Amplitude | A | ||||
| Wellenlänge | λ | ||||
| Abstand, Entfernung | x | ||||
| Durchmesser | d | ||||
| Länge | l | ||||
| Gangunterschied | δ | ||||
| s | Sekunde | Zeit | - | Periodendauer | T |
| Schwebungsdauer | TS | ||||
| Nachhallzeit | TH | ||||
| Dämpfungsgrad | D | ||||
| K | Kelvin | Temperatur | - | ||
| kg | Kilogramm | Masse | - | Masse | m |
| je Meter | 1/m | Wellenzahl | k | ||
| Schalldämpfungskoeffizient | α | ||||
| Ausbreitungskoeffizient | γ | ||||
| - | Quadratmeter | Fläche | m2 | durchschallte Fläche | S |
| Querschnitt(sfläche) | |||||
| - | Kubikmeter | Volumen | m3 | ||
| rad | Radiant | ebener Winkel | m / m | Phasenwinkel | |
| Einfallswinkel | α | ||||
| Reflexionswinkel | α' | ||||
| Brechungswinkel | β | ||||
| Hz | Hertz | Frequenz | 1/s | Frequenz | f |
| Abklingkoeffizient | δ | ||||
| - | Meter je Sekunde | Geschwindigkeit | m/s | Schallgeschwindigkeit | c |
| Schallschnelle | v | ||||
| - | Radiant je Sekunde | rad/s = m/(m·s) | Kreisfrequenz | ω | |
| - | Kubikmeter je Sekunde | m3/s | Schallfluss | q | |
| - | Dichte | kg/m3 | |||
| - | kg/s | Dämpfungskonstante | b | ||
| N | Newton | Kraft | (m·kg)/s2 | äußere Kraft | Fext. |
| Normalspannung | σ | ||||
| Pa | Pascal | Druck | N/m2 = kg/(m·s2) | Schalldruck | p |
| Komperssionsmodul | K | ||||
| Elastizitätsmodul | E | ||||
| - | m2/N = (m·s2)/kg | Dehnungszahl | α | ||
| Kompressibilität | k | ||||
| J | Joule | Arbeit, Energie | Nm = (kg·m2)/s2 | ||
| W | Watt | Leistung | J/s = (kg·m2)/s3 | Schalleistung | P |
| - | Watt je Quadratmeter | W/m2 = kg/s3 | Schallintensität | J | |
| - | Joule je Kubikmeter | J/m3 = kg(m·s2) | Schalldichte | w | |
| - | kg/(m2·s) | Schallkennimpedanz | Z | ||
| - | (N·s)/m5 = kg/(m4·s) | akustische Impedanz | Za | ||
| - | J/K kg = m2/(s2·K) | spezifische Gaskonstante | Ri |
=> zum Inhalt
| e | Eulersche Zahl | Basis des Natürlichen Logarithmus | e = 2,718 281 828 ... |
| π | Pi | Ludolfsche Zahl | π = 3,141 592 654 ... |
=> zum Inhalt
Seit Huygens werden Logarithmen für das musikalische Rechnungswesen verwendet. Der Vorteil besteht darin, dass das Rechnen selbst erleichtert wird (umständliche Multiplikationen werden durch einfachere Additionen ersetzt) und dass durch das weitgehend logarithmische Verhalten der Hörempfindung ein angemessenerer Vergleich zwischen Berechnung und Hörerfahrung möglich ist. Ein Nachteil zeigt sich bei der Logarithmierung von Frequenzverhältnissen (z.B. Cent-Skala), da der Konsonanzgrad nicht mehr anhand kleiner ganzer Zahlen abgelesen werden kann.
Leonhard Euler empfahl den Logarithmus zur Basis 2, was zur Berechnung von Frequenzverhältnissen vorteilhaft ist. Die Oktave hat den Wert 1 erhält; gleiche Intervalle verschiedener Oktaven die gleiche Mantisse haben und sich nur durch die Kennziffer unterscheiden.
Definition: Der Logarithmus von b (Numerus, Logarithmand) zur Basis a ist die reele Zahl c (Exponent), für die gilt:
loga b = c ↔ ac = b a > 0, a ≠ 1, b > 0
Praktische Verwendung finden Logarithmen zur
Basis 10 Dekadischer oder Briggscher Logarithmus lg (auch log oder log10)
Basis e Natürlicher oder Neperscher Logarithmus ln (auch loge)
Basis 2 Dualer oder binärer Logaritmus ld (auch lb oder log2)
Rechenregeln für Logarithmen:
loga 1 = 0 loga a = 1 loga ax = x
loga (x · y) = loga x + loga y loga (x/y) = loga x - loga y
loga xn = n · loga x loga x1/n = 1/n loga x loga c = 1 / logc a
loga c · logc a = 1
Umrechnung unterschiedlicher Basen:
logb x = (loga x) / (loga b)
Umrechnungsfaktoren:
ld x = M2 · lg x M2 (Zweiermodul) = 3,321 928 094 949 (= ld 10)
lg x = M · ln x M (Modul) = 0,434 294 (= lg e = 1 / ln 10)
ln x = 1 / M · lg x 1 / M = 1,302 585 (= 1 / lg e = ln 10)
=> zum Inhalt
|
a |
Mann |
|
|
engl. lunch (kurzer, dunkler a-Laut |
|
e |
lebendig |
|
Rettich, Hände |
|
|
æ |
engl. catch, hand (heller, offener ä-Laut) |
|
i |
Rivale |
|
o |
Krokodil |
|
Horn |
|
|
ø |
König |
|
œ |
Förster |
|
u |
Kuriosität |
|
y |
Mücke |
=> zum Inhalt
|
Α |
α |
alpha |
Η |
η |
eta |
Ν |
ν |
ny |
Τ |
τ |
tau |
|
Β |
β |
beta |
Θ |
ϑ θ |
theta |
Ξ |
ξ |
xi |
Υ |
υ |
ypsilon |
|
Γ |
γ |
gamma |
Ι |
ι |
iota |
Ο |
ο |
omikron |
Φ |
phi |
|
|
Δ |
δ |
delta |
Κ |
κ |
kappa |
Π |
Π |
pi |
Χ |
χ |
chi |
|
Ε |
ε |
epsilon |
Λ |
λ |
lambda |
Ρ |
ρ |
rho |
Ψ |
ψ |
psi |
|
Ζ |
ζ |
zeta |
Μ |
μ |
my |
Σ |
σ ς |
sigma |
Ω |
ω |
omega |
=> zum Inhalt => weiter
 © 2005 Everard Sigal
© 2005 Everard Sigal