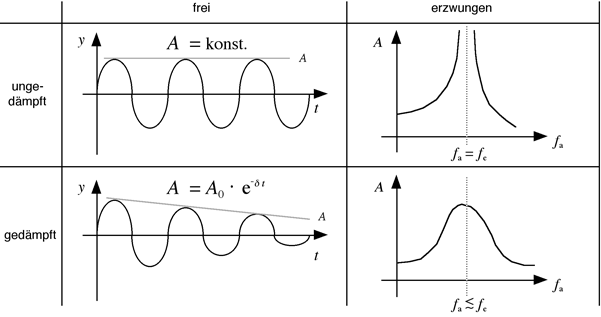
Periodische Schwingungen sind zeitlich-periodische Zustandsänderungen eines Systems in gleichen Zeitabständen.
Ein System, das in der Lage ist Schwingungen auszuführen, heißt Oszillator.
Bei ungleichen Zeitabständen liegt eine nichtperiodische Schwingung vor.
Unter Zustandsänderungen ist abwechselnde Zu- und Abnahme mechanischer, elektrischer oder thermischer Zustände zu verstehen. Für die Musik sind vorwiegend Zustandsänderungen mechanischer und elektrischer Natur von Bedeutung.
[Beispiel] Auch Erdumdrehung, Herzschlag und Atmung sind - wenn auch sehr langsame - periodische Schwingung. Das anschaulichste Beispiel für periodische Schwingungen ist ein Uhrenpendel. Beim sogenannten Sekundenpendel dauert eine vollständige Schwingung zwei Sekunden. Die Schwingungsdauer von Uhrenpendeln ist allein von ihrer Länge und der Erdanziehungskraft, nicht aber von der Masse abhängig.
Damit Schwingungen entstehen können, muss das System durch eine äußere Störung (Anstoß) aus seinem Gleichgewichtszustand (Ruhelage) gebracht werden und es müssen Kräfte vorhanden sein, die das System wieder in Richtung der Ruhelage bewegen (Rückstellkräfte).
Unter Ruhelage versteht man den Zustand eines Oszillators bevor eine äußere Störung stattfindet.
Rückstellkräfte sind im Oszillator vorhandene Kräfte, die auf die Ruhelage gerichtet sind.
Ein aus der Ruhelage gebrachter Oszillator hat das Bestreben, in die Ruhelage zurückzukehren.
Jede mechanische Schwingung ist eine ständige Umwandlung von kinetischer in potentielle Energie und umgekehrt.
[Beispiel] Die Pendelbewegung vedeutlicht dies: Beim Durchgang durch die Ruhelage hat das Pendel seine höchste Geschwindigkeit und damit ausschließlich kinetische Energie. Sie geht über in potentielle Energie, wenn sich das Pendel dem höchsten Punkt seines Ausschlags zubewegt und dabei verlangsamt. Im Umkehrpunkt der Bewegung ist die Geschwindigkeit auf Null gesunken und damit die kinetische Energie vollständig in potentielle Energie umgewandelt. Dieser Vorgang wiederholt sich ständig, solange das Pendel schwingt.
Man unterscheidet:
|
freie Schwingungen: |
bei einmaliger Anregung des Oszillators schwingt dieser mit seiner Eigenfrequenz. Er steht nicht in Verbindung mit anderen Oszillatoren, die die Schwingung beeinflussen können. |
|
[Beispiel] Angeschlagene Klaviersaiten schwingen mit ihren Eigenfrequenzen. |
|
|
erzwungene Schwingungen (→ [7]): |
bei denen der Oszillator ständig durch eine äußere periodische Kraft angeregt wird |
|
[Beispiel] Schwingungen des Resonanzkörpers einer Geige bei anhaltendem Ton |
|
|
gedämpfte Schwingungen (→ [4]): |
bei denen der Oszillator durch Reibung ständig Energie an die Umgebung abgibt |
|
[Beispiel] Eine angeschlagene Glocke gibt ihre Schwinungsenergie durch Reibung an die umgebende Luft ab und wird dadurch zunehmend leiser. |
|
|
selbsterregte Schwingung: |
wenn einem Oszillator die während einer Periode verlorengegangene Energie von einer inneren Energiequelle wieder zugeführt wird (Rückkopplung → [13]) |
|
[Beispiel] Uhrpendel, das von Steigrad und Anker ständig zum Schwingen angeregt wird. Auch das periodisch sich öffnende und schließende Rohrblatt einer Klarinette sorgt für den Ersatz der verlorengegangenen Energie und erhält somit die Schwingung aufrecht. |
|
Abb. [2]-1: Zusammenhang zwischen freier, erzwungener, gedämpfter und ungedämpfter Schwingung
Die Auslenkung des Oszillators zu einem bestimmten Zeitpunkt (also sein Abstand von der Ruhelage) heißt Elongation.
Formelzeichen: y Einheit: m [Meter oder davon abgeleitete Einheit]
In der Ruhelage ist der Betrag der Elongation Null. Bei der Elongation handelt es sich um einen Momentanwert, der vom Zeitpunkt der Beobachtung abhängig ist.
Die Amplitude ist der Betrag der weitesten Elongation (= Maximalwert der Elongation).
Formelzeichen: A Einheit: m [Meter oder davon abgeleitete Einheit]
[2-1] A = ymax.
Eine Periode ist eine vollständige Schwingung.
Sind aufeinanderfolgende Schwingungen in ihrem Verlauf gleich, spricht man von rein periodischer Schwingung.
Unter Periodendauer versteht man den zeitlichen Abstand zwischen zwei gleichen aufeinander folgenden Schwingungszuständen.
Formelzeichen: T Einheit: s [Sekunde]
Die Frequenz ist die Anzahl der Perioden pro Sekunde. Sie gibt an, wie oft sich ein periodischer Vorgang pro Sekunde wiederholt.
Formelzeichen: f Einheit: Hz [Hertz = s-1]
Für besonders große Frequenzen wird als Einheit kHz [Kilohertz = 1 000 Hz], MHz [Megahertz = 1 Million Hz] oder GHz [Gigahertz = 1 Milliarde Hertz] verwendet.
Frequenz und Periodendauer lassen sich in Beziehung bringen:
Frequenz = Kehrwert der Periodendauer
Periodendauer = Kehrwert der Frequenz
[2-2] 
=> zum Inhalt
Die einfachste Form einer Schwingung ist die Sinusschwingung. Der Verlauf einer Sinusschwingung läßt sich mathematisch mit einer gleichförmigen Kreisbewegung (Rotation) beschreiben. Dabei wird die Kreisbewegung auf eine senkrecht zur Kreisbahn stehende Ebene projiziert. Ein Punkt P führt eine Kreisbewegung aus, wobei sich der lotrechte Abstand zum Kreisdurchmesser ständig ändert. Dieser Abstand entspricht der Elongation.
[Beispiel] Das Kreisen der Pedale beim Radfahren - mit Blick in Fahrtrichtung betrachtet - zeigt eine regelmäßige Auf- und Abbewegung.
Die Elongation y beträgt zu einem beliebigen Zeitpunkt:
[3-1] 
Abb. [3]-1: Projektion der Kreisbewegung in die Ebene (Sinus-Funktion)
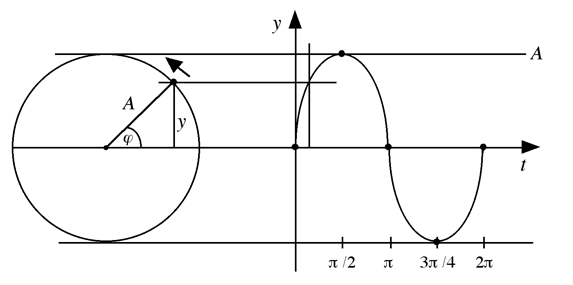
A ist der Radius des Kreises (Amplitude) und gleichzeitig die größte lotrechte Abstand vom Kreisdurchmesser.
Mit Phasenwinkel wird der Winkel zwischen Radius und Kreisdurchmesser bezeichnet.
Formelzeichen: 
Einheit: rad [Radiant]
Eine vollständige Schwingung (also eine ganze Umdrehung) entspricht einem Winkel von 360° (im Bogenmaß: 2π)
Da eine Schwingung T Sekunden dauert, wird in einer beliebigen Zeit t der Winkel
[3-2] 
durchlaufen.
Die Kreisfrequenz ist der Quotient aus einer vollständigen Rotation (2π) und der Periodendauer.
Formelzeichen: ω Einheit: rad/s [Radiant je Sekunde]
[3-3] 
Unter Phasenverschiebung 
versteht man den Wert des Phasenwinkels zum Zeitpunkt t0 (Beginn der Beobachtung der Schwingung):
[3-4] 
Je nach dem Wert der Phasenverschiebung nennt man die Phase voreilend (
> 0) oder nacheilend ( < 0).
Als Funktion der Zeit läßt sich die Elongation mit Phasenverschiebung ausdrücken:
[3-5] 
=> zum Inhalt
Beim Erregen einer Schwingung wird dem Oszillator Energie zugeführt. Sobald die Erregung aufhört, verliert der Oszillator die zugeführte Energie im wesentlichen durch Reibung. Die mechanische Energie der Schwingung wird dabei in Wärmeenergie umgewandelt. Die Folge ist, dass die Amplitude der Schwingung ständig abnimmt und der Oszillator schließlich aufhört zu schwingen. Dieser Vorgang heißt Dämpfung.
Abb. [4]-1: gedämpfte Schwingung
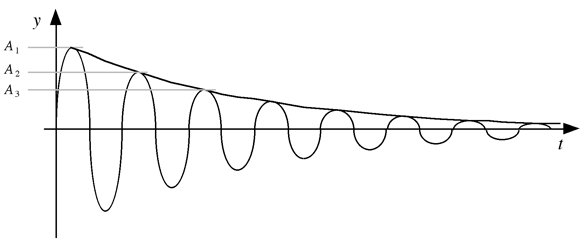
Am häufigsten erfolgt die Amplitudenabnahme in Form einer geometrischen Reihe. Dabei stellt der Quotient zweier aufeinanderfolgender Amplituden eine Konstante dar, die man Dämpfungsverhältnis nennt.
Formelzeichen: k Einheit: 1
[4-1]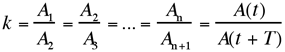 
Der natürliche Logarithmus des Dämpfungsverhältnisses wird logarithmisches Dekrement genannt.
Formelzeichen: Λ Einheit: 1 Maß: Np [Neper]
[4-2] 
Für kleine Dämpfungen gilt: 
d : Verlustfaktor
Der Verlustfaktor wird definiert:
Formelzeichen: d Einheit: 1
Verlustfaktor = doppelter Dämpfungsgrad
[4-3] 
Die Güte ist der Kehrwert des Verlustfaktors:
Formelzeichen: Q Einheit: 1
[4-4] 
Wird der Briggsche Logarithmus des Dämpfungsverhältnisses angegeben, spricht man von Abklingmaß.
Formelzeichen: Λ Einheit: 1 Maß: dB [Dezibel]
[4-5] 
k : Dämpfunsverhältnis
Die Periodendauer einer gedämpften Schwingung ist geringer als die Periodendauer der entsprechenden ungedämpften Schwingung.
Für die Elongation einer gedämpften Schwingung zum Zeitpunkt t gilt:
[4-6] 
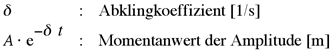
Der Dämpfungsgrad ist die Kenngröße für die Dämpfung eines Schwingungssystems.
Formelzeichen: D Einheit: s [Sekunde]
[4-7] 
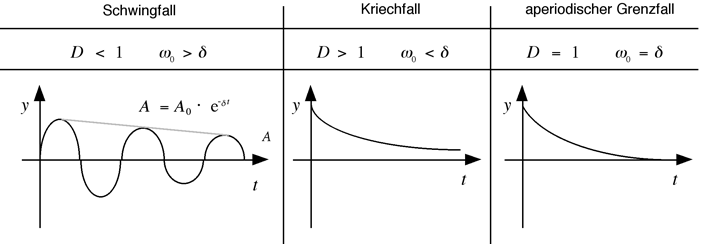
Je nach Wert des Dämpfungsgrades spricht man von
|
Schwingfall |
D < 1 |
|
|
Kriechfall |
D > 1 |
es tritt keine Schwingung auf,die Amplitude nimmt monoton ab |
|
aperiodischer Grenzfall |
D = 1 |
es tritt eben keine Schwingung mehr auf |
Kommt die Schwingung durch sehr große Dämpfung schon nach einer halben Periode zur Ruhe, spricht man von aperiodischer Schwingung.
Abb. [4]-2
Die Abklingzeit eines Schwingungssystems ist die Zeit, in der die Amplitude einer Schwingung auf 1/e (= 0,37; e: Eulersche Zahl) des Ausgangswertes abgesunken ist. In der Akustik wird meist die Nachhallzeit angegeben.
Formelzeichen: τ Einheit: s [Sekunde]
[4-8] 
Der Abklingkoeffizient ist der Quotient aus Dämpfungskoeffizient und doppelter Masse:
Formelzeichen: δ Einheit: 1/s [je Sekunde]
[4-9] 
=> zum Inhalt
Zusammengesetzte Schwingungen entstehen durch Superposition (additive Überlagerung) zweier oder mehrerer Sinusschwingungen (Partialschwingungen). Es ergibt sich eine resultierende Schwingung (Resultierende).
Die Superposition von Sinusschwingungen gleicher Frequenz heißt Interferenz. Die Resultierende ist ebenfalls sinusförmig.
Zwei Schwingungen mit gleicher Phase bezeichnet man als gleichphasig, mit unterschiedlicher Phase als phasenverschoben um die Phasendifferenz .
[5-1] 
Abb. [5]-1: Superposition zweier Schwingungen mit
gleicher Frequenz und Phase aber unterschiedlicher Amplitude
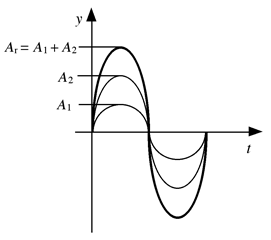
Wenn sich zwei gleichfrequente Sinusschwingungen mit gleicher Phase und gleicher Amplitude überlagern, hat die Resultierende die doppelte Amplitude (Verstärkung).
[5-2] 
Bei Überlagerung zweier gleichfrequenter Sinusschwingungen mit gleicher Amplitude aber einer Phasendifferenz 
von π, 3π, 5π, ... (Phasenopposition), ist die Amplitude der Resultierenden Null, d. h. die beiden Schwingungen löschen sich gegenseitig aus (Auslöschung).
[5-3] 
[Experiment] Eine Stimmgabel besteht aus zwei gegeneinander schwingenden Stäben. Die von den beiden Stäben ausgesandten Schallwellen überlagern sich. Wenn eine angeschlagene Stimmgabel vor dem Ohr um ihre Achse gedreht wird, verstärken sich die Schallwellen oder löschen sich gegenseitig aus, was sich in einer permanenten Lautstärkeänderung während der Drehung bemerkbar macht.
Bei Überlagerung von Sinusschwingungen ungleicher Frequenz ist die Resultierende in den meisten Fällen nicht sinusförmig.
Werden zwei Schwingungen, deren Frequenzen f1 und f2 sich nur geringfügig unterscheiden, überlagert, ändert sich die Amplitude der Resultierenden periodisch (Schwebung). Die Anzahl der Änderungen pro Sekunde heißt Schwebungsfrequenz (fs). Die Schwebungsfrequenz ist der Betrag der Differenz der beiden Partialschwingungen und tritt als Hüllkurve, die die Amplituden der Resultierenden umhüllt in Erscheinung. Es gilt:
[5-4] 
Die Frequenz der Resultierenden fr ist der Mittelwert der Frequenzen der beiden Partialschwingungen.
[5-5] 
Abb. [5]-2: Schwebung
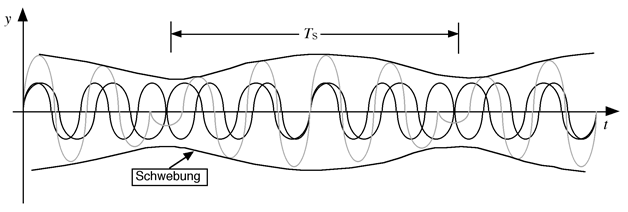
In den Schwebungsminima zeigt die Resultierende Phasensprünge (Drehung der Phase um 180°).
Die Schwebungsdauer ist der zeitliche Abstand zweier minimaler Amplituden der Schwebung (Kehrwert der Schwebungsfrequenz).
Formelzeichen: Ts Einheit: s [Sekunde]
[5-6]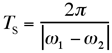 
Sind die Amplituden der beiden Partialschwingungen gleich, löschen sie sich bei Phasenopposition aus. Bei Gleichphasigkeit erreicht die Amplitude der Resultierenden das Doppelte der Amplitude einer der beiden Partialschwingungen (vollkommene Schwebung).
Eine Schwebung ist bei einer Schwebungsfrequenz von 1 - 8 Hz als ständig schwankende Lautstärkeänderung zu hören. Die beiden Partialschwingungen werden nicht getrennt wahrgenommen, sondern als nur eine. Wächst die Zahl der Phasensprünge pro Sekunde über 10, empfindet das Ohr eine zunehende „Rauhigkeit“, bis schließlich zwei verschiedene Töne wahrgenommen werden.
Sind die Amplituden der Partialschwingungen ungleich, geht die Amplitude der Resultierenden im Minimum auf die Differenz der Amplituden der beiden Partialschwingungen zurück.
Das Phänomen der Schwebung läßt sich beim Einstimmen von Musikinstrumenten nutzen: werden beide Frequenzen solange angenähert, bis die Schwebungsfrequenz 0 Hz beträgt, sind sie frequenzgleich (Schwebungsnull).
Zusammengesetzte Schwingungen lassen sich auf zwei Arten graphisch darstellen:
Bei einem Sonogramm wird sowohl die Zeitfunktion (also die zeitabhängige Änderung) als auch die Zusammensetzung eines zu untersuchenden Klangs dargestellt: die Spektrallinien zeigen in ihrer unterschiedlichen Dicke den Amplitudenverlauf der entsprechenden Frequenzen.
=> zum Inhalt
Mit Hilfe der harmonischen Analyse (Fourier-Analyse) wird eine beliebige periodische nicht sinusförmige Schwingung eindeutig in eine Summe von (meist unendlich vielen) harmonischen Schwingungen zerlegt.
Dabei wird davon ausgegangen, dass die zu betrachtende Schwingung aus einer Grundschwingung mit einer bestimmten Grundfrequenz und Oberschwingungen mit Frequenzen, die ganzzahlige Vielfache der Grundfrequenz sind, zusammengesetzt ist.
Die Grundschwingung wird auch als 1. Harmonische, die 1., 2., 3., ..., n. Oberschwingung als 2., 3., 4., ..., n. Harmonische bezeichnet.
Die Elongation einer Bewegung beträgt zu einem bestimmten Zeitpunkt t (Fourier-Reihe):
[6-1]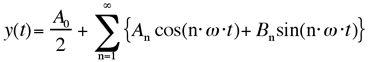 
mit den Fourier-Koeffizienten:
[6-2]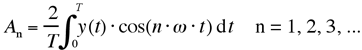 
[6-3]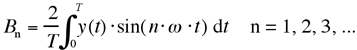 
Unberücksichtigt bleiben die Phasen der Partialschwingungen, die für die akustisch-physiologische Empfindung zusammengesetzter Schwingungen ohnehin keine praktische Bedeutung hat. Das menschliche Gehör nimmt Phasenverschiebungen zwischen Partialschwingungen im allgemeinen nicht wahr: es wird ein und derselbe Klang empfunden.
Besondere zusammengesetzte Schwingungen sind Sägezahn-, Rechteck- und Dreieckschwingung:
Abb. [6]-1: Sägezahn-, Rechteck- und Dreieckschwingung
=> zum Inhalt
Wird ein Körper durch Einwirkung einer äußeren Kraft Fext. zum Schwingen angeregt und dann sich selbst überlassen, vollführt er Eigenschwingungen einer bestimmten Eigenfrequenz fe, die von der schwingenden Masse und vom Betrag der Rückstellkraft abhängig ist. Jedes schwingfähige System besitzt eine Eigenfrequenz. Je geringer die Dämpfung des Systems, desto stärker wirkt sich die Eigenfrequenz aus.
Die Amplitude der erzwungenen Schwingung ist proportional zur Amplitude der äußeren Kraft.
Erfolgt die Schwingungserregung periodisch mit einer Anregungsfrequenz fa, so nimmt der Oszillator diese Frequenz an und die Eigenfrequenz wird unterdrückt. Ein auf diese Weise angeregter Oszillator heißt Resonator. Die Schwingungen, die er ausführt sind erzwungene Schwingungen. Die Zeit, die verstreicht bis der Resonator die Anregungsfrequenz angenommen hat, heißt Einschwingvorgang. Solange sich die erzwungene Schwingung nicht ändert, spricht man von stationärer Phase.
Abb. [7]-1: Schwingungsverlauf einer erzwungenen Schwingung
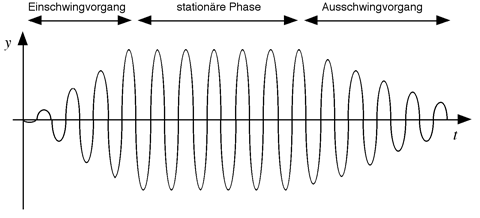
Der Einschwingvorgang spielt beim Erkennen von Intrumentenklangfarben eine entscheidende Rolle.
Unter Phasenverschiebung versteht man die Phasendifferenz zwischen Anregung und erzwungener Schwingung.
Verschwindet die anregende Kraft, schwingt der Körper in seiner Eigenfrequenz weiter und erfährt im Normalfall eine Dämpfung. Dieser Vorgang heißt Ausschwingvorgang.
Wächst die Anregungsfrequenz, so nimmt die Amplitude des Resonators zunächst zu. Wenn die Anregungsfrequenz der Eigenfrequenz entspricht, ist die maximale Amplitude erreicht. Dieser Punkt heißt Resonanz zwischen Eigenschwingung und erzwungener Schwingung. Bei weiterer Erhöhung der Anregungsfrequenz nimmt die Amplitude der erzwungenen Schwingung wieder ab.
Bei einem gedämpften System wird das Amplitudenmaximum nicht erst bei Erreichen der Eigenfrequenz, sondern schon früher erreicht. (→ Abbildung [2]-1, unten rechts)
Durch Resonanz kann Materie zerstört werden (Resonanzkatastrophe).
[Beispiel] Nierensteinzertrümmerung - Brückeneinsturz durch Wind
=> zum Inhalt => weiter
© 2005 Everard Sigal