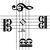B.4. musikalische Akustik – Tonsysteme

[16] Tonsysteme

Innerhalb des Frequenzbereichs des hörbaren Schalls (16 Hz - 20 kHz) liegen unendlich viele Tonhöhen. Nur eine begrenzte Auswahl davon, der bestimmte Ordnungsprinzipien zu Grunde liegen, wurde in allen vergangenen und wird in bestehenden Kulturen in der Musik verwendet.
Diese begrenzte Zahl von untereinander abhängigen Tönen nennt man Tonsystem.
Ein Tonsystem ist gekennzeichnet durch die Intervalle, die zwischen seinen Tönen bestehen.

Den Abstand (Frequenzverhältnis) zweier Töne nennt man Intervall.

Zwei Intervalle werden addiert (der obere Ton des unteren Intervalls wird unterer Ton des oberen), indem man ihren Frequenzverhältnisse multipliziert. Das Ergebnis ist die Summe der beiden Intervalle.

Die Intervalladdition wird auch Aneinanderreihung genannt.

[Beispiel] Aneinanderreihung zweier Quinten (3:2):

              Quinte + Quinte = (3:2) · (3:2) = 9:4

Geht man vom Ton c aus, erhält man durch die erste Quinte den Ton g, durch die zweite Quinte über g den Ton d1.

Zwei Intervalle werden subtrahiert (der obere Ton beider Intervalle ist der gleiche), indem man ihre Frequenzverhältnisse dividiert (mit dem Kehrwert multipliziert). Auf diese Weise erhält man die Differenz der beiden Intervalle.

[Beispiel] um den Ton d1 aus dem obenstehenden Beispiel in die eingestrichene Oktave zu verlegen, subtrahiert man eine Oktave (2:1):

              doppelte Quinte - Oktave = (9:4) / (2:1) = (9:4) · (1:2) = 9:8

Erstes Ordnungsprinzip (in nahezu allen Kulturen) ist die Oktavidentität von zwei Tönen. Das Phänomen Oktavidentität bedeutet, dass zwei Töne unterschiedlicher Höhe den gleichen Charakter haben. Infolgedessen erhalten sie auch die gleiche Bezeichnung.

Zwei Töne bilden das Intervall der Oktave, wenn ihre Frequenzen ein Verhältnis von 2:1 aufweisen.

Zwischen zwei Tönen im Oktavabstand wird eine je nach Tonsystem wechselnde Anzahl von Tönen, die in bestimmten Verhältnissen (Proportionen) stehen, eingeschaltet.
Maßgeblich für die Anzahl der Töne in einer Oktave sind:

• die Grenzen des Unterscheidungsvermögens für Tonhöhen
• Beschaffenheit und Handhabbarkeit der Musikinstrumente
• historischer und kultureller Stand der Entwicklung einer Kultur

Das Ordnungsprinzip der Töne beruht auf mathematischen Proportionen, die einen unterschiedlichen Grad der Verwandtschaft der Töne untereinander erklären.

Für den musikalischen Gebrauch wiederum wird meist nur eine nach bestimmten Ordnungsprinzipien getroffene Auswahl aus den im Tonsystem zur Verfügung stehenden Tönen verwendet. Diese Auswahl bezeichnet man als Tongeschlecht (Modus); nach Tonhöhen geordnet als Tonleiter. Eine Tonleiter endet mit der Wiederkehr der Oktave des Ausgangstones. Die Töne einer Tonleiter werden Stufen genannt. Ein bestimmter Ton (Hauptton) als Ausgangspunkt für die Tonleiter lässt eine Tonart entstehen.

Zweites Ordnungsprinzip (im wesentlichen der europäischen Kulturen, von denen im Folgenden ausschließlich die Rede sein wird) ist das Intervall der Quinte.

Die Frequenzen zweier Töne im Quintabstand verhalten sich 3:2.

Die Quinte ist das Intervall mit der nach der Oktave einfachsten Proportion. In der Obertonreihe tritt dieses Verhältnis zwischen dem 3. und 2. Partialton auf und liefert den ersten vom Grundton verschiedenen Ton.

Das Prinzip der Quintverwandtschaft zweier Töne wird nach dem griechischen Philosophen Pythagoras pythagoreisches Prinzip genannt.

Pythagoras und die Pythagoreer machten ihre Versuche zu Intervallverhältnissen auf dem Monochord (Einsaiter), einem Instrument, das aus einem Resonanzkasten und nur einer darübergespannten Saite besteht. Die Saite lässt sich durch einen verschiebbaren Steg in unterschiedliche Verhältnisse teilen. Betrachtet wurden die Proportionen der durch Abteilung entstandenen Saitenlängen, nicht die Frequenzen. Da sich aber Saitenlänge und Frequenz umgekehrt proportional verhalten, gelten für Längen- und Frequenzverhältnisse die gleichen Proportionen.

Das pythagoreische Tonsystem entwickelt alle seine Töne durch fortwährendes Quintieren (Aneinanderreihung vom Quinten, Quintgeneration).

In der Pentatonik werden fünf Töne durch Aneinanderreihung von vier Quinten gewonnen:

In eine Oktave versetzt (als fünfstufige Tonleiter):

Die Heptatonik (sieben Töne) entsteht durch Aneinanderreihung von sechs Quinten:

In eine Oktave gelegt ergibt sich die diatonische pythagoreische Tonleiter:

Reihe V₁ gibt die Frequenzverhältnisse bezogen auf den Hauptton an; Reihe V₂ das Frequenzverhältnis zweier benachbarter Stufen der Tonleiter.

In dieser Tonleiter gibt es zwischen zwei benachbarten Stufen nur zwei verschieden große Schritte:

   pythagoreische große Sekunde (natürlicher Ganzton):     9:8

   pythagoreisches Limma (pythagoreischer diatonischer Halbton):     256:243

Weiter als bis zur Fünfteilung der Saite gingen die Pythagoreer nicht.

Die Aneinanderreihung weiterer fünf Quinten liefert zwölf Töne, die die Oktave nahezu in gleichgroße Intervalle teilt:

In eine Oktave versetzt ergibt sich die chromatische pythagoreische Tonleiter:

Die zwischen benachbarten Stufen auftretenden Schritte sind:

   pythagoreisches Limma (pythagoreischer diatonischer Halbton):       256:243

   pythagoreische Apotome (pythagoreischer chromatischer Halbton):  2187:2048

Eine weitere Quinte ergibt den Ton eis⁷ ((3:2)_¹¹) mit dem Verhältnis 177147:2048. Die Differenz zwischen eis (sieben Oktaven subtrahiert: 177147:131072) und f (4:3) bezeichnet man als Pythagoreisches Komma (PK). Es hat ein Frequenzverhältnis von

Die beiden nur um das PK differierenden Töne werden enharmonische Töne genannt.

Weitere (im Prinzip unendlich viele) Quinten führen zu insgesamt in der Notenschrift darstellbaren 35 Tonstufen, wobei zu den zwölf chromatischen Tönen 23 enharmonische treten.

Ein weiteres Ordnungsprinzip ist die Harmonische Teilung der Oktave. Dabei wird das arithmetische Mittel von Zähler und Nenner eines Frequenzverhältnisses (a/c) gebildet (die Summe von Zähler und Nenner werden halbiert). Das Ergebnis ist eine Zahl b zwischen a und c.

     b = (a + c)/2     Harmonische Teilung (arithmetisches Mittel)

[Beispiel] Teilung der Oktave (2:1 = 4:2): a = 4; c = 2

            b = (4 + 2) / 2 = 6 / 2 = 3

            a : b = 4:3 (Quarte) und b : c = 3:2 (Quinte)

Die Oktave (2:1) wird in Quinte (3:2) und Quarte (4:3) geteilt,

die Quinte in große Terz (5:4) und kleine Terz (6:5)

die große Terz in großen Ganzton (9:8) und kleinen Ganzton (10:9).

---------------------------- 2:1 ----------------------------

------------- 3:2 ----------------- ------------ 4:3 --------

------- 5:4 ------ ---- 6:5 -------

 9:8        10:9   16:15      9:8

Dieses Prinzip führt zur reinen Stimmung. Sie geht auf Didymos Chalkenteros zurück, der mit diesem Tonsystem die als unrein erachtete pythagoreische große Terz (81:64) durch die natürliche (reine) große Terz (5:4, erhalten durch die Fünfteilung der Saite) ersetzte.

Die Differenz zwischen diesen beiden Terzen [(81/64):(5/4)] heißt Didymisches Komma (DK). Es hat ein Frequenzverhältnis von

Die pythagoreische große Terz wurde deshalb als unrein erachtet, weil ihr Verhältnis aus großen Zahlen besteht und einem Intervall eine um so größerer Konsonanzgrad zugesprochen wurde, je kleiner die Zahlen sind, die ihr Verhältnis bilden. Als ebensowenig konsonant galt die pythagoreische große Sexte (27:16). Sie wurde ersetzt durch die bei der Fünfteilung der Saite auftretende Proportion 5:3 (natürliche große Sexte = reine Terz über der Quarte). Auch die pythagoreische große Septime (243:128) wurde ausgetauscht, und zwar gegen die natürliche (reine) (größere) große Septime (15:8), die als Terz über der Quinte [(3/2)·(5/4)] berechnet wurde.

Als vollkommenste Konsonanz galt die Oktave (2:1), es folgten Quinte (3:2) und Quarte (4:3).

Die reine diatonische Tonleiter hat folgende Frequenzverhältnisse:

Die zwischen benachbarten Stufen auftretenden Schritte sind:

  natürlicher kleiner Ganzton              10:9

  natürlicher großer Ganzton                 9:8

  natürliche (kleinere) kleine Sekunde 16:15

Nachteil der reinen Stimmung ist die Tatsache, dass (wie aus V₂ ersichtlich) zwei unterschiedliche große Sekunden auftreten.

Das pythagoreische Prinzip und die harmonische Teilung (und die daraus resultierende reine Stimmung) versuchen das in der westlichen Musik schon vor diesen existierende fünfstufige, siebenstufige (diatonische) bzw. zwölfstufige (chromatische) Tonsystem zu erklären und berechenbar zu machen.

Dass nicht mehr als 12 Tonhöhen in einer Oktave verwendet werden, obwohl eine weitaus größere Zahl gehörsmäßig unterschiedbar ist, liegt in der Tatsache begründet, dass eine geringere Anzahl die Vielfalt der melodischen und harmonischen Kombinationsmöglichkeiten stark einschränken, bei einer größeren Anzahl dagegen die Vielfalt unüberschaubar würde. Die Zwölfstufigkeit ist ein der Verarbeitungskapazität des menschlichen Gehirns angemessenes Tonsystem.

Ab dem 15. Jahrhundert wurden Versuche angestellt, die Oktave in mehr als zwölf Stufen zu teilen (z.B. 17, 19, 31, 34, 50 oder 70).

=> zum Inhalt 

[17] Temperatur

Tonsysteme beschreiben die Verwandschaftsgrade der Töne unabhängig von einer absoluten Tonhöhe. Für den konkreten Fall des Musizierens wird ein Ton absolut festgelegt (Stimmton) und alle anderen Töne danach berechnet. Diesen Vorgang nennt man Stimmen.

Unter Temperatur versteht man den Versuch, die Töne eines Tonsystems so einzustimmen, dass einerseits möglichst (viele) reine Intervalle entstehen, andererseits jeder Ton nur einmal vertreten ist. Im wesentlichen läuft das darauf hinaus, das PK auf mehrere Intervalle zu verteilen, damit möglichst viele Tonarten gleichermaßen brauchbar sind.

Die Stimmung des siebenstufigen (diatonischen) Tonsystems erfolgte im Mittelater nach der pythagoreischen Stimmung (PS); die des zwölfstufigen (chromatisch-enharmonischen) Tonsystems in Renaissance und Generalbasszeitalter nach der mitteltönigen Temperatur (MT) und seit dem ausgehenden 18. Jahrhundert nach der gleichschwebenden Temperatur (GT). Daneben gab und gibt es sogenannte Ausnahmestimmungen.

Das Bestreben der MT ist es, möglichst viele reine Terzen (5:4) zu erhalten.

Sie geht auf Arnold Schlick zurück (1511, Spiegel der Orgelmacher und Organisten): alle Terzen werden rein gestimmt, das DK wird auf vier Quinten verteilt. Die Bezeichnung „mitteltönig“ bezieht sich auf die große Sekunde, die mit ihrem Frequenzverhältnis zwischen dem kleinen (10:9) und großen (9:8) Ganztonschritt angeordnet wird.

Pietro Aron (1523, Thoscanello de la musica) stimmt die Terz C-E rein und verteilte je 1/4 DK auf die Quinten C-G/G-D/D-A/A-E (mittlere Abweichung von der GT: 20 Cent)

Francisco de Salinas (1577, De musica libri septem) konstruierte ein Cembalo mit 19 Tasten je Oktave und verteilte 1/3 DK (mittlere Abweichung von der GT: 30 Cent)

Gottfried Silbermann entwickelte eine MT mit 1/6 DK (mittlere Abweichung von der GT: 9,3 Cent)

Henricus Grammateus (1518, Ayn new kunstlich Buech) ging von der pytagoreischen Stimmung aus und stimmte die chromatischen Töne als geometrisches Mittel der angrenzenden diatonischen Töne (mittlere Abweichung von der GT: 3,3 Cent)

Die Temperatur von Andreas Werckmeister (1691, Musikalische Temperatur, Oder deutlicher und wahrer Mathematischer Unterricht, Wie man ... Ein Klavier ... wohl temperiert stimmen können) stimmt acht von zwölf Quinten rein und verteilt das PK auf die verbleibenden vier Quinten.

Eine durch Temperatur entstandene besonders unreine Quinte heißt Wolf.

Der Versuch der musikalisch-akustische Realisierung der Harmonischen Teilung ist die reine Stimmung.

Die letzte Konsequenz aller Versuche zu einer praktischen wie logischen Temperatur führen zur gleichschwebenden Temperatur. Bei der gleichschwebenden Temperatur wird die Oktave in zwölf gleichgroße Halbtonschritte geteilt, das heißt das PK wird auf alle zwölf Quinten gleichmäßig verteilt. Das Frequenzverhältnis zweier Töne im Halbtonabstand beträgt:

→ Tabelle der Frequenzverhältnisse der GT in Anhang.

In der GT sind alle Intervalle außer der Oktave mehr oder weniger gegenüber der PT und der RT verstimmt; dafür tauchen des PK und das DK nicht mehr auf, alle Tonarten sind gleichermaßen brauchbar. Die Bezeichnung „gleichschwebend“ bezieht sich auf diese Tatsache: da alle gleichen Intervalle gleich groß sind, ist auch die Schwebungsfrequenz zwischen den Obertönen gleich.

Zur Distanzmessung der Tonhöhendifferenz zweier Tönen führte A. J. Ellis 1885 die Cent-Skala ein. Dabei wird ein Halbton der gleichschwebenden Temperatur in 100 Cent geteilt. 1200 Cent ergeben also eine Oktave. Diese Skala sagt nichts über den Verwandtschaftsgrad zweier Töne aus, ist aber hilfreich bei der Beschreibung außereuropäischer Tonsysteme.

[17-1]       T = 3986 lg (f₁ / f₂) = 1200 ld (f₁ / f₂) cent

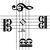  © 2005 Everard Sigal